「C++极简教程」第二章 C++控制结构

2.1 算法与流程图（不展开讲）

2.2 C++中的语句

语句是C++程序的最基本单位，以分号结束。

注：头文件包含属于编译预处理，不是C++语句。

1
2

#include <iostream> //头文件包含不是语句
int a; //是语句

1. 声明语句

用来定义或声明变量和函数。

1

int a, b;

2. 表达式语句

完成计算和操作。

1

c = a + b;

3. 控制语句

用来完成对程序流程的控制。

如：if 语句、for 语句、while 语句等。

4. 函数调用语句

用来完成函数的调用。

1

strcpy(a, b);

5. 空语句

单独分号构成的语句。

意义：用在无内容可写，却需要语句来进行填充的位置。常见于循环语句，注意和分号区分。

6. 复合语句

由一对{}构成，用来包括多个语句。

• 形式：{语句1; 语句2;}

1
2
3
4

if(i <= 100) //该段语句只是示例，无实际意义
{
    a = b + c;
}

• 意义：用在只需要一个语句，但单个语句无法满足需求。
• 注：在语法上复合语句认为是一条语句。

2.3 分支结构

1. if语句

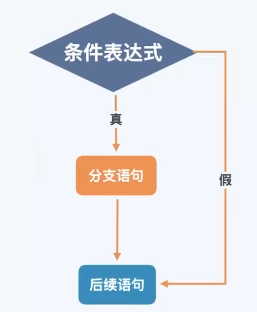
(1) 单分支if语句

1
2

if(表达式)
	语句; 

解释：表达式一般为逻辑或关系表达式，如果结果为true，则运行语句。而如果表达式是其他类型，则自动转换，非0为true，0为false。

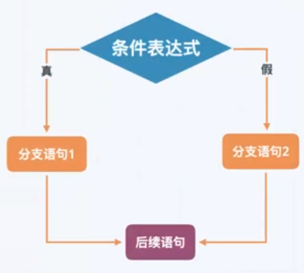
(2) 双分支if语句

1
2
3
4

if(表达式) 
	语句1;
else
	语句2;

解释：如果表达式结果为true，则运行语句1，反之运行语句2。

例：闰年判断（4倍数一般是闰年，整百数必是400倍数才是闰年）

1
2
3
4
5
6

int year;
cin >> year;
if(year % 4 == 0 && year % 100 != 0 || year % 400 == 0)
	cout << year << “是闰年” << endl;
else
	cout << year << “不是闰年” << endl;

注：if语句的嵌套

if语句的分支语句可以是一个新的if语句，叫做if语句的嵌套。

借助if的嵌套可以实现多分支的判断功能。

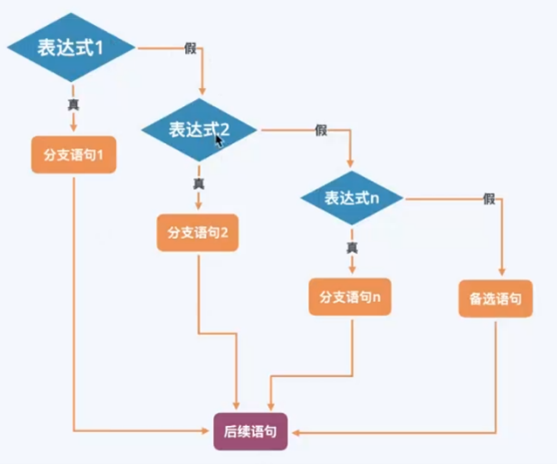
A. 嵌套在else语句：阶梯式if语句

1
2
3
4
5
6
7

if(表达式)
	语句1;
else if(表达式2)
	语句2;
else if……
else
	语句n;

解释：依次对各个表达式进行判断，如果有满足true的则执行对应语句，并终止整个语句。

（注意和hoi4伪语言区分开）

B. 嵌套在if语句：在if分支语句中增加新的if语句（不推荐）

• C++规定了if和else的“就近配对”原则，即相距最近且还没有配对的一对if和else首先配对。

  1 2 3 4 5 6

  if(表达式1) if(表达式2) 语句1; else 语句2; //else将与第二个if匹配。

• 如果需要强行更改配对关系，则要将属于同一层的语句放在{}中。

  1 2 3 4 5 6 7 8

  if(表达式1) { if(表达式2) 语句1; } else 语句2; //else将与第一个if匹配。

2. 条件运算符 ?:

三目运算符?:可以简化if语句表达。

1

表达式1 ? 表达式2 : 表达式3;

解释：判定表达式1，若成立则执行表达式2，不成立则执行表达式3。

注：

• 条件运算符中后两个表达式的类型和第一个表达式完全无关。
• 条件运算符等级仅高于赋值（15）。
• 条件运算符是右结合性，自右向左结合。
  • 例：a ? b : c ? d : e 应该理解为 a ? b : (c ? d : e)

3. switch语句

1
2
3
4
5
6
7

switch(整型表达式)
{
case 常量表达式1 :《语句序列1》《break;》// 《》是“可选”的意思
……
case 常量表达式n :《语句序列n》《break;》
《default : 语句序列》
}

解释：

1. 计算switch后的整型表达式值。

2. 逐个匹配case后表达式的值，如果相等则执行对应的语句序列。

3. 如果语句后有break则终止整个switch语句，否则继续执行后续语句序列且不再进行判断。

4. 若所有case都无法匹配则执行default语句。

例：计算学生的成绩等级

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

int score;
cout << "请输入学生的成绩:"; cin >> score;
switch(score/10)
{
case 10: case 9:
	cout << "该生成绩为A" << endl; break;
case 8:
	cout << "该生成绩为B" << endl; break;
case 7:
	cout << "该生成绩为C" << endl; break;
case 6:
	cout << "该生成绩为D" << endl; break;
default:
	cout << "该生成绩为E" << endl; 
}

注：

• switch语句只能对整数和字符类型使用。
• 只能判断表达式是否相等，不能判定不等大于小于。
• case后的表达式只能是常量表达式。
• break语句的使用请务必注意。

2.4 循环结构

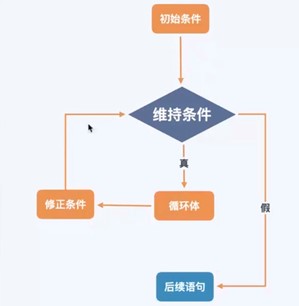
1. while语句

1
2

while(表达式)
	循环体语句;

解释：如果满足表达式则反复执行循环体语句直到不满足表达式为止。

例：求解1~100的和

1
2
3
4
5
6
7
8

const int n=100; //用常变量利于修改程序
int i=1, sum=0; //循环初始条件
while(i <= n) //循环入口条件
{
	sum+=;//循环体
    ++i;//循环修正条件
}
cout << "sum=" << sum << endl;

解析：

1. 代码结束后i的值为101。

2. sum=0不能遗忘，否则会出现随机数。

3. 做题看结果通常看头尾。

4. 若循环体中有多个语句一定要用{}。

5. 部分题目中会将循环修正条件放入循环入口条件中，即将循环体中的i++放入while(i++<=n)中，但一般不推荐这样写。

2. do-while语句

1
2

do 循环体语句
while(表达式);

解释：先做一次循环体语句，若表达式满足则继续循环，直到表达式不满足终止循环；若表达式不满足则不执行循环。

注：do-while语句与while语句的区别

• do-while语句至少执行一次循环体后再判断循环条件是否满足。
• while语句先判断条件，然后才执行循环体，可能一次都不执行。

例：求解1~100的和

1
2
3
4
5
6
7
8
9

const int n=100;//用常变量利于修改程序
int i=1, sum=O;//循环初始条件
do
{
	sum+=i;//循环体
	i++;//循环修正条件
}
while(i<=n);//循环入口条件
cout << "sum=" << sum << endl;

3. for语句

1
2

for (表达式1; 表达式2; 表达式3)
	循环体语句;

解释：先执行式1，然后判断式2，真则执行循环体，后执行式3，接着重复判断式2，直到2为假结束整个循环。

注：

• 相对于while，式1相当于初始条件；式2相当于维持条件；式3相当于修正条件。
• for语句中只有式2是判定条件。
• for语句中三个表达式都可以为空，但是分号**;**一定要有。
• 省去1可以将初始条件放在for之前，省去3可以将修正条件放在循环体中，而省去2则表达式2的值将默认为true，必须用其他方法结束循环。

例：求解1~100的和

1
2
3
4
5

const int n=100; //用常变量利于修改程序
int i, sum=O;
for(i=1;i<=n;++i)
    sum += i;
cout << sum << endl;

4. 三种循环的选择与注意

​ A．三种循环语句没有本质区别，可以互相代替。

​ B．当循环起点和终点值直接确定，推荐使用for语句。

​ C．若终止条件不明确（如等待某值输入），推荐while语句。

​ D．do-while语句最典型场合是必须至少执行一次的循环。如展示菜单。

​ E．若循环外还要用某变量，则该变量不能在for()和while()语句中定义。

5. 循环语句的嵌套

当循环语句中的循环体中又有循环语句时，就构成了嵌套循环。

理解：以时钟的时针和分针为例：

时针每移动一格（大循环），分针就必须跑完一圈（小循环）。

解释：大循环每进行一次，小循环就完整循环一次。

注：大小循环的运行可能相关也可能不相关。

经典案例：打印问题

• 主要思想：利用循环算法，打印各种有规律的数字或图形。
• 基本思路：行是大循环，列是小循环。首先断定打印的行数，然后在每一行当中确定打印的列数以及每一列的空格和内容。行数、列数以及打印内容往往存在关联，需要分析清楚并用来控制循环的次数。

算法示例：

1
2
3
4
5
6
7
8

for (int i = 1; i <= 4;++i)
{
	for (int j = 1; j <= i; ++j)
		cout << ' ';
	for (int j = 1; j <= 7; ++j)
		cout << '*';
	cout << '\n';
}

解析：

1. 首先确定行数为4行。

2. 每行包括前面空格后面*号。

3. 空格数量和行号相等。

4. *号的数量是固定为7个。

5. 打印完每一行之后要换行。

6. 循环中的控制语句

(1) break语句

• 在循环语句中遇到break，整个循环结束。
• 如果有多层循环嵌套，则break只结束最近的循环。

例：素数判断

基本思路：i从2到根号n之间进行循环，将每个i用n去除，如果可以整除则直接判断不是素数；如果i的整个循环走完仍不能整除才能判断n是素数。

1
2
3
4
5
6
7
8
9
10
11

int n, k, i;
cout << "输入整数n:" ;
cin >> n;
k = sqrt(1.0 * n);
for (i = 2; i <= k; ++i)
	if (n % i == 0)
		break;
if(i > k)
	cout << "是素数\n";
else
	cout <<"不是素数\n";

(2) continue语句

在循环语句中遇到continue，当轮循环停止，立即开始下一轮循环。

例：输出100以内的偶数。

1
2
3
4
5

for (i = 1; i <= 100; i++)
{
if ( i % 2 != 0 ) continue;
	cout<< i << endl;
}

注：break与continue的区别：

​ break终止整个循环，而continue只是终止一次循环。

2.5 C++常用基本算法

1. 穷举法

• 主要思想：列出问题的所有可能性，按所需条件进行逐一筛选。
• 要求：在设计算法时，应尽可能减少循环的次数以提高效率。

(1) 素数问题

点击跳转

(2) 水仙花数问题

问题说明：如果一个三位数等于其各位数字的立方和，则该数为水仙花数。

问题思路：将所有的三位数用条件进行验证即可

代码：

1
2
3
4
5
6
7
8
9

int i, a, b, c; //a,b,c分别为百位、十位、个位
for(i=100; i<=999; i++)
{
    a = i/100;
    b = (i-a*100)/10;
    c = i - a*100 - b*10;
    if(i==a*a*a+b*b*b+c*c*c)
        cout << i << '\t'
}

(3) 完全数问题

问题说明：如果一个数等于其所有因子（自身除外）的和，则该数为完全数。

如：6=1+2+3，28=1+2+4+7+14

问题思路：遍历一个数的所有因子，并将其求和之后判断与自己是否相等即可。

问题要点：如何遍历一个数的所有因子？

A.单个数的判断：

1
2
3
4
5
6
7
8
9

int i, n, s=0; //注意s必须初始化为0
cin >> n;
for(i=1; i<=n/2; i++)
	if(n%i==0)
		s += i;
if(s==n)
    cout << "该数是完全数\n";
else
    cout << "该数不是完全数\n";

B.遍历指定区间的完全数：（以1000以内为例）

• 未优化代码：正确但运算次数大，判断需要进行n/2次循环。

1
2
3
4
5
6
7
8
9
10

int i, n, s;
for(i=1; n<=1000; n++)
{
    s = 0; //注意s必须在此处初始化，对每一个n，s都应该重置为0开始
    for(i=1; i<=n/2; i++)
        if(n%i==0)
            s += i;
    if(s==n)
    	cout << n << "\t";
}

• 代码优化：当区间过大的时候，将其从2到根号n进行循环，每次求和的时候同时加上成对因子，但如果有重复的因子需去除。

1
2
3
4
5
6
7
8
9
10
11
12

int i, n, k, s=1; //因子必定有1，将s初始化为1减少一次循环
cin >> n;
k = sqrt(n);
for(i=2; n<=k; i++)
    if(n%i==0)
        s += i + n/i;
	if(k*k == n)
        s -= k; //关键！！k为平方数时会出现一个重复因子i = n/i故要减一次
    if(s==n)
    	cout << "该数是完全数\n";
	else
    	cout << "该数不是完全数\n";

(4) 简单推理问题

例：某同学做了好事但不留名。校长问了4个人:A说不是我，B说是C，C说是D，D说C胡说。已知4人中有3人说的是真话，请问做好事的是谁?

问题思路：遍历所有可能做好事的人，统计说真话的人是否为3个即可。

问题要点：如何用程序来计算和统计本问题的真假？

1
2
3
4
5
6

char man;
for(man = 'A'; man <='D'; man++)
{
if((man!='A')+(man=='C') +(man=='D')+(man!='D')== 3 ) //3个bool=1
cout<<"好人就是"<<man<<endl;
}

2. 递推法

• 主要思想：按照某种规律，对同一个变量不断更改其值（递推），从而求解问题。
• 基本思路：确定递推项 → 确定递推起点 → 分析递推规律 → 判断终止条件

(1) 斐波那契数列

数列背景︰

数列1，1，2，3，5，8…为以意大利数学家费波纳切命名的数列。
定义小兔子t时间后长为大兔子，大兔子会繁殖且繁殖周期为t。
则1对小兔子t时间后长大为1对大兔子。
t时间后变成2对（1对小1对大）。
t时间后变成3对（2对大1对小）。
t时间后变为5对（3对大2对小）等等。

问题背景：现用循环求出该数列的前n项。

问题思路：不可能定义n个变量逐个保存，只能用少数的变量反复使用来达到该效果。

问题要点：如何找出递推的变化规律?务必通过该问题，掌握递推算法的核心思想。

斐波那契数列递推思路：

1. 确定递推项：三项f1，f2，f3

2. 递推起点：f1=f2=1

3. 递推规律：f3=f1+f2，然后旧f2推出新f1，旧f3推出新f2，再重复前述过程

   例：(右上到左下替换)

   f1	f2	f3
   1	1	2
   1	2	3
   2	3	5

4. 终止条件：指定次数（本例为n-2次）

解法一：

1
2
3
4
5
6
7
8
9
10

int f1=1, f2=1, f3, i; //只定义3个变量
cout << f1 << '\t' << f2 << '\t'; //打印开始
for(i=3; i<=20; i++) //打印前20个值
{
	f3 = f1 + f2; //打印结果
    cout<<f3<<'\t';
	if(i%5==0) //每5个数换一行
	cout << endl;
	f1 = f2; //变量递推，准备下一次的值
    f2 = f3; //变量递推，顺序问题很重要

解法二：

​ 递推规律：新f1=旧f1+旧f2；新f2=新f1+旧f2

1
2
3
4
5
6
7

int f1=1, f2=1, i;
for(i=1; i<=10; i++)
{
	cout << f1 << '\t' << f2 << '\t';
    f1 = f1 + f2;
	f2 = f1 + f2;
} //请对照递推规律自行理解体会该思路

(2) sin(x)的求解问题

已知 sin(x) = x - x³ / 3! + x⁵ / 5! - x⁷ / 7! + …..
利用该公式求解sin(x)的值，精度为10^-6。

问题思路：观察每一项的分子、分母和符号位的值。当前项的符号位乘 -1 就是下一项的符号位；当前项的分子乘 x² 就是下一项的分子;当前项的分母乘以(2*n+1)*(2*n)，即为下一项的分母，n为当前的项数。

精度为10^-6可用来控制循环的终止，如果计算的通项绝对值小于该值，则循环终止。

示例：求 sin 3 = ?

1
2
3
4
5
6
7
8
9

double x = 3, s = 0, t = x;
int n = 1;
while(fabs(t) >= 1e-6)
{
	s += t;
	t = -t * x * x / (2 * n + 1) / (2 * n);
    ++n;
}
cout << s << endl;

(3) 二分法求解方程问题

问题说明：假设f(x)在区间[a,b]中单调递增，且肯定有根，求解该根的值。

问题思路：取区间的一半判断其函数值，如果为负，则收缩区间为中点到右区间，反之为左区间到中点。重复上述过程，直到中点值为0或满足精度要求即可。

问题要点：反复递推区间的左右值即可，当求出的中点值小于某区间即可终止。

示例：二分法求x²-2=0

1
2
3
4
5
6
7
8
9
10

double a=0,b=2,c=(a+b)/2; //递推起点
double t = c*c-2;
while(fabs(t)>=1e-6)//终止条件 不能写t!=0，因计算机中t实际不能达到精确的0
{
	if(t>0) b=c; //递推过程1
	else a=c; //递推过程1
	c=(a+b)/2; //递推过程2
	t = c*c-2;
}
cout << c << endl;

(4) 整数分解问题

问题说明：输入任意正整数，判断其位数、计算各位数字之和、求解其倒序数、判断是否为回文数等问题。

问题思路：从个位数开始依次提取，其方法是对10求余，然后将该数除以10，并重复上述步骤，直到该数为0则结束。

问题要点：上述思路仅限分解，如果是组装则逆向进行。

示例：求解12345的倒序数。

1
2
3
4
5
6
7

int n = 12345,m = 0;
do
{
	m = m * 10 + n % 10; //n%10求解末位数，n/=10将末位向左移一位从而循环
	n /= 10;
} while (n > 0);
cout << m << '\n';

3. 模拟法

基本思想：根据题目给出的规则，对题目要求的相关过程进行模拟。模拟法对于步骤比较繁杂的问题比较合适。

报数问题

题目：小张按1～20报数，小李按1～30报数，若两人同时开始，并以同样速度报数，当两人都报了1000个数时，报相同数字的次数有多少?

思路：进行1000次循环，每一次小张和小李各报一次数（注意调整下一次的值），统计相等次数即可。

1
2
3
4
5
6
7
8
9

int round, zhang = 0, wang = 0, count = 0;
for (round = 1; round <= 1000; ++round)
{
	++zhang; ++wang;
    if(zhang == wang) ++count;
    if(zhang == 20) zhang = 0;
    if(wang == 30) wang = 0;
}
cout << count;